Propagating the Uncertainties on the Effective Area (Aeff)
When evaluating the systematic uncertainties due to the effective area, the flux(source_name, emin, emax) method available in pyLikelihood must not be used. The systematic uncertainty must be calculated using the spectral parameter values in the output xml files.
If N is the normalization of the source, one obtains:
ϵsyst,max(min) = |Nmax(min) - Nnom|/Nnom
where Nnom is the best-fit value obtained without any scaling file while Nmax(min) is the one obtained using the max(min) scaling files.
The value of ϵsyst,max(min) can be used to calculate the systematic uncertainty on the flux F:
Fsyst,max(min) = (1 ± ϵ)syst,max(min)Fnom
This is strictly valid if the normalization of the source is fitted only, otherwise parameter correlation should be taken into account.
As for any data analysis, it is important to consider the systematic errors when performing a LAT analysis. An overview of the sources of systematic errors in the LAT can be found on the caveats page. Among the sources of systematic errors related to our imperfect knowledge of the performance of the instrument, the most important one is due to innaccuracies in the effective area.
The systematic uncertainty on the effective area is modeled by ε(E), the maximal relative difference to the nominal effective area Aeffnom. As explained in the caveats page, the LAT team has estimated ε(E) by performing several consistency checks between data and IRF predictions. ε(E) depends on how the analysis is performed, as shown in the following figure and table:
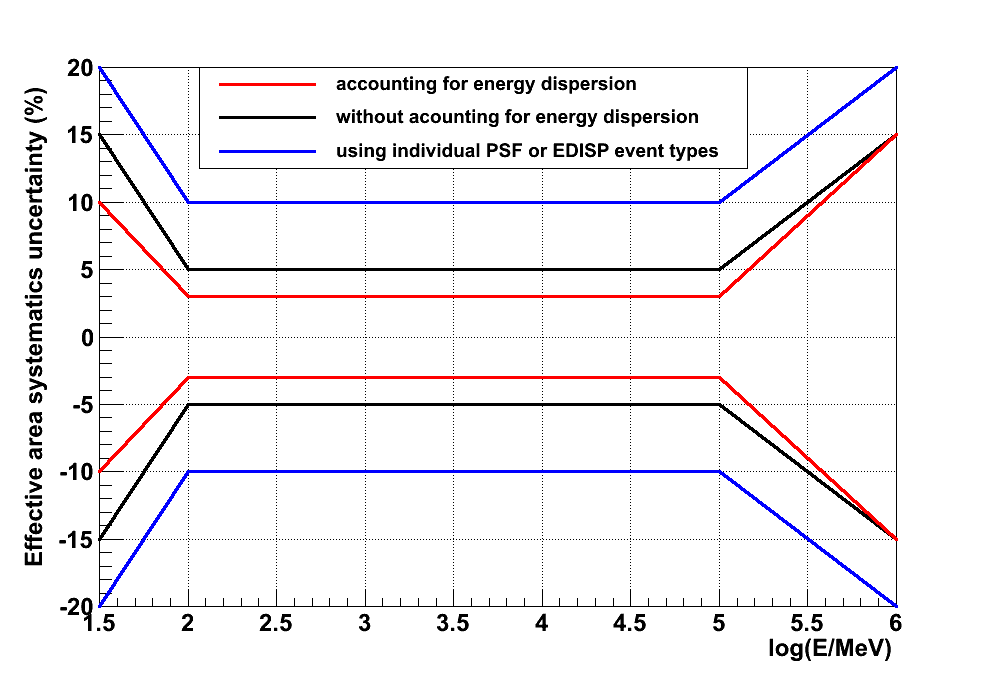
| Aeff Uncertainty Functions | ||||
|---|---|---|---|---|
| Selection (see caveats for more information) | Plot | E = 30-100 MeV | E = 100 MeV - 100 GeV | E > 100 MeV |
| FRONT, BACK, FRONT+BACK, Joint Analyses (w/ edisp) | Red Curve | 3% + 14% x (2.0-log(E/MeV)) | 3% | 3% + 12% x (log(E/MeV)-5) |
| FRONT, BACK, FRONT+BACK, Joint Analyses (w/o edisp) | Black Curve | 5% + 20% x (2.0-log(E/MeV)) | 5% | 5% + 10% x (log(E/MeV)-5) |
| PSF and EDISP Types (Individual) | Blue Curve | 10% + 20% x (2.0-log(E/MeV)) | 10% | 10% + 10% x (log(E/MeV)-5) |
One has to keep in mind that ε(E) defines an envelope in which any function is a valid effective area displacement (though we do not expect extremely abrupt changes with energy; going from min to max should not occur within less than 0.5 in log(E)). As a result, for any function f(E) with |f(E)| < ε(E), (1+f(E)) x Aeffnom is a possible valid effective area. The choice of f(E) depends on the analysis, as will be explained below (see bracketing Aeff).
- the Galactic diffuse model
- the isotropic diffuse model
- source spectral parameters in a LAT source catalog
Thus, to perform a fully consistent spectral analysis with Aeffsys, one would have to rederive all of the information about the above sources (i.e. derive new Galactic and isotropic diffuse models and a new source catalog). This is computationally prohibative and, fortunately, there is a simple way to overcome this difficulty. Let's consider for instance S, a catalog source in the source model, which spectral parameters are held fixed in the fit to the catalog values. These spectral parameters were derived in the catalog analysis, that is to say that they were the result of a spectral analysis of a ROI containing this source S. Because the catalog analysis used Aeffnom, the spectral parameters are such that the convolution of the source spectrum with Aeffnom predicts the correct number of counts due to source S. As a consequence, using these spectral parameters with a different Aeff would predict a wrong number of counts. Since the goal of fixing the spectral parameters of S to the catalog ones is to ensure the prediction of the correct number of counts from S, "one can see that one should always use Aeffnom for this source S, regardless if one is assessing the effect of Aeffsys. This reasoning holds for the case in which only the normalization parameter of source S is free in the fit. Because f(E) can depend on E, it induces a change in the spectral shape that can not be absorbed by the freedom of the normalization parameter in order to predict the correct number of counts as a function of energy.
Practically, when performing a spectral analysis of a ROI with a non nominal effective area Aeffsys, one has to use Aeffsys with the sources for which all spectral parameters are free, and Aeffnom for all the other sources in the source model (including the Galactic and isotropic diffuse models because they contain spectral shape information that can not be modified).
Starting with the Fermitools, a mechanism for evaluating the Aeff systematics has been implemented which allows the user to modulate the effective area for an individual source. It is done by giving the possibility to specify the scaling (1+f(E)) for each source. The scaling is given in a scaling file which is just a text file with two columns, energy in MeV and the relative scaling of the effective area. Because points are interpolated on a log-log grid (i.e., a power-law is used to interpolate between points), it is strongly recommended to use a rather fine log(E) binning (a good rule of thumb is at least 15 bins per decade).
The path of the scaling file is given in the scaling_file attribute of the spectrum element in the XML definition of a source, as shown in the following example:
<source name="Mrk 421" type="PointSource"> <spectrum scaling_file="scaling_function.txt" type="PowerLaw2"> <parameter free="1" max="1e+10" min="0" name="Integral" scale="1e-07" value="1.3" /> <parameter free="1" max="-1" min="-5" name="Index" scale="1" value="-1.6" /> <parameter free="0" max="200000" min="20" name="LowerLimit" scale="1" value="100" /> <parameter free="0" max="200000" min="20" name="UpperLimit" scale="1" value="100000" /> </spectrum> <spatialModel type="SkyDirFunction"> <parameter free="0" max="360" min="-360" name="RA" scale="1" value="166.1138" /> <parameter free="0" max="90" min="-90" name="DEC" scale="1" value="38.2088" /> </spatialModel> </source>
If no scaling file is defined in the XML definition, the nominal Aeff is used by default.
Bracketing Aeff
Because any reasonably smooth function f(E) with |f(E)| < ε(E) can be used to define a possible valid effective area Aefsys = (1+f(E)) x Aeffnom, the user has to choose a set of functions f(E) to assess the systematic uncertainties. The LAT team recommends to use the so-called bracketing Aeff method. It consists, for any given observable (flux, spectral index or cutoff, etc...), the 2 functions f(E) that maximize the negative and positive variations of this quantity. The exact choice of the functions is left to the user since it strongly depends on the observables that are measured. For instance, in order to estimate the systematic uncertainty on a spectral break or cutoff, one should choose functions that flip from - ε(E) to ε(E) or from ε(E) to - ε(E) around the measured value of the cutoff or break.
The most extreme cases in terms of total Aeff variations (but not in terms of spectral variations) are the ones in which f(E) correspond to + and - ε(E). As examples we provide the scaling files for the extreme cases:
| Example Scaling Files | |
|---|---|
| Selection (see caveats for more information) | File Function |
| FRONT, BACK, FRONT+BACK, Joint Analyses (w/ edisp) | min max |
| FRONT, BACK, FRONT+BACK, Joint Analyses (w/o edisp) | min max |
| PSF and EDISP Types (Individual) | min max |
