Source Model Definitions for gtlike
This page describes the Spectral and Spatial Models available for use in gtlike.
Two types of sources can be defined, PointSource and DiffuseSource. Each type of source model is comprised of a spectral and a spatial model component, where each component is made up of several parameters.
Each model parameter has a range of valid values that can be specified, and is described by a set of attributes. The actual value of a given parameter that is used in the calculation is the value attribute multiplied by the scale attribute. The value attribute is what the optimizers see. Using the scale attribute is necessary to ensure that the parameters describing the objective function, -log(likelihood) for this application, all have values lying roughly within an order-of-magnitude of each other. The free attribute determines whether the parameter will be allowed to be fixed or free in the fitting process.
NOTE: Free flag attributes are currently disabled for spatial model parameters since fitting for these parameters has not been implemented (primarily due to the enormous overhead associated with computing the energy-dependent response functions for each source component).
Spectral Models
Several spectral functions are available for use with gtlike. For point source spectral models, the units are ![]() . For diffuse sources, the units are
. For diffuse sources, the units are ![]() .
.
The available point source spectral models are:
PowerLaw:
Example: XML Model Definition
This function has the form:
![]()
where the parameters in the XML definition have the following mappings:
- Prefactor =

- Index =
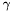
- Scale =
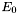
BrokenPowerLaw:
Example: XML Model Definition
This function has the form:
![]()
where
- Prefactor =

- Index1 =
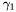
- Index2 =
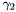
- BreakValue =

PowerLaw2:
Example: XML Model Definition
This function uses the integrated flux as a free parameter rather than the Prefactor:
![]()
where
- Integral =
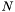
- Index =
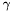
- LowerLimit =
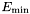
- UpperLimit =
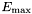
NOTE: The UpperLimit and LowerLimit parameters are always treated as fixed and, as should be apparent from this definition, the flux given by the Integral parameter is over the range (LowerLimit, UpperLimit). Use of this model allows the errors on the integrated flux to be evaluated directly by likelihood, obviating the need to propagate the errors if one is using the PowerLaw form.
BrokenPowerLaw2:
Example: XML Model Definition
Similar to PowerLaw2, the integral flux is the free parameter rather than the Prefactor:
![]()
where
![\[ \newcommand{\emin}{{E_{\rm min}}} \newcommand{\emax}{{E_{\rm max}}} \newcommand{\pfrac}[2]{\left(\frac{#1}{#2}\right)} \newcommand{\Int}{{\displaystyle\int}} N_0(N, E_{\rm min}, E_{\rm max}, \gamma_1, \gamma_2) = N \times \left\{\begin{array}{ll} \left[ \Int_\emin^\emax \pfrac{E}{E_b}^{\gamma_1} dE\right]^{-1} & \mbox{$\emax < E_b$}\\ \left[ \Int_\emin^\emax \pfrac{E}{E_b}^{\gamma_2} dE\right]^{-1} & \mbox{$\emin > E_b$}\\ \left[ \Int_\emin^{E_b} \pfrac{E}{E_b}^{\gamma_1} dE + \Int_{E_b}^\emax \pfrac{E}{E_b}^{\gamma_2} dE \right]^{-1} & \mbox{otherwise}\end{array}\right. \]](./images/src_analysis/form_31.png)
and
- Integral =
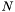
- Index1 =
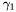
- Index2 =
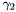
- BreakValue =

- LowerLimit =
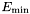
- UpperLimit =
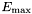
SmoothBrokenPowerLaw:
Example: XML Model Definition
![\[ \newcommand{\pfrac}[2]{\left(\frac{#1}{#2}\right)} \frac{dN}{dE} = N_0 \pfrac{E}{E_0}^{\gamma_1}\left(1+\pfrac{E}{E_b}^\pfrac{\gamma_1-\gamma_2}{\beta}\right)^{\beta} \]](./images/src_analysis/form_50.png)
where
- Prefactor =

- Index1 =
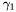
- Scale =
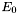
- Index2 =
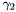
- BreakValue =

- beta =
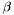
LogParabola:
Example: XML Model Definition
This model is typically used for modeling Blazar spectra.
\[\frac{dN}{dE} = N_0 \left( \frac{E}{E_b} \right)^{-(\alpha + \beta\ln(E/E_b))} \]
where
- norm = \(N_0\)
- alpha = \(\alpha\)
- beta = \(\beta\)
- Eb = \(E_b\)
Note: \(E_b\) is a scale parameter that should be set near the lower energy range of the spectrum being fit and is usually fixed. See Massaro et al., A&A (2004) 413, 489.
ExpCutoff:
Example: XML Model Definition
An exponentially cut-off power-law used for modeling blazar spectra subject to absorption by the extragalactic background light (EBL).
\[\frac{dN}{dE} = N_0 \times \left\{ \begin{array}{ll} \left(\frac{E}{E_0}\right)^\gamma & \mbox{$E < E_b$}\\ \left(\frac{E}{E_0}\right)^\gamma \exp\left[ - ( (E - E_b)/p_1 + p_2\ln(E/E_b) + p_3\ln^2(E/E_b) ) \right] & \mbox{otherwise} \end{array} \right. \]
where
- Prefactor =

- Index =
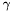
- Scale =
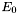
- Ebreak =

- P1 =
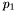
- P2 =
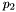
- P3 =

BPLExpCutoff:
Example: XML Model Definition
An exponentially cut-off broken power-law.
![\[ \newcommand{\pfrac}[2]{\left(\frac{#1}{#2}\right)} \newcommand{\eabs}{{E_{\rm abs}}} \frac{dN}{dE} = N_0 \times \left\{\begin{array}{ll} \pfrac{E}{E_b}^{\gamma_1} & \mbox{$E < E_b$ and $E < \eabs$}\\ \pfrac{E}{E_b}^{\gamma_2} & \mbox{$E > E_b$ and $E < \eabs$}\\ \pfrac{E}{E_b}^{\gamma_1}\exp[-(E - \eabs)/p_1] & \mbox{$E < E_b$ and $E > \eabs$}\\ \pfrac{E}{E_b}^{\gamma_2}\exp[-(E - \eabs)/p_1] & \mbox{$E > E_b$ and $E > \eabs$}\end{array}\right. \]](./images/src_analysis/form_39.png)
where
- Prefactor =

- Index1 =
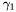
- Index2 =
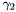
- BreakValue =

- Eabs =
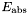
- P1 =
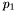
PLSuperExpCutoff:
Example: XML Model Definition
For modeling pulsars. Note that the PLSuperExpCutoff spectral shape in the 4FGL corresponds to PLSuperExpCutoff2 in the Fermitools (see next entry).
\[{dN \over dE} = N_0 \left( {E \over E_0}\right)^{\gamma_1} exp\left( - \left({E \over E_c}\right)^{b} \right)\]where
- Prefactor =\(N_0\)
- Index1 = \(\gamma_1\)
- Scale = \(E_0\)
- Cutoff = \(E_c\)
- Index2 = \(b\)
PLSuperExpCutoff2:
Example: XML Model Definition
For modeling pulsars.
\[{dN \over dE} = N_0 \left( {E \over E_0}\right)^{\gamma_1} exp\left( -aE^{b} \right)\]
where
- Prefactor = \(N_0\)
- Index1 = \(\gamma_1\)
- Scale = \(E_0\)
- Expfactor = \(a\)
- Index2 = \(b\)
PLSuperExpCutoff3:
Example: XML Model Definition
For modeling pulsars.
\[{dN \over dE} = N_0 \left( {E \over E_0}\right)^{\gamma_0 + bc} exp\left( c \left( 1 - \left({E \over E_0}\right)^b \right) \right)\]
where
- Prefactor = \(N_0\)
- IndexS = \(\gamma_0\)
- Scale = \(E_0\)
- Expfactor2 = \(c\)
- Index2 = \(b\)
Note:
- \(N_0\) is the normalization (flux density) at \(E_0\).
- \(\gamma_0\) is the local spectral index at \(E_0\).
These features are shared by the LogParabola functional.
PLSuperExpCutoff4:
Example: XML Model Definition
For modeling pulsars.
\[\frac{dN}{dE} = \begin{cases} N_0 \left( \frac{E}{E_0} \right)^{\gamma_0-\frac{d}{2}\ln\frac{E}{E_0} - \frac{db}{6} \ln^2\frac{E}{E_0} - \frac{db^2}{24} \ln^3\frac{E}{E_0}} , & \text{if}\ |b \ln\frac{E}{E_0}|<1e^{-2} \\ N_0 \left( \frac{E}{E_0} \right)^{\gamma_0+d/b} exp \left( \frac{d}{b^2} (1-( \frac{E}{E_0} )^b ) \right) & \text{otherwise} \end{cases}\]
where
- Prefactor = \(N_0\)
- IndexS = \(\gamma_0\)
- Scale = \(E_0\)
- ExpfactorS = \(d\)
- Index2 = \(b\)
Note:
- \(N_0\) is the normalization (flux density) at \(E_0\).
- \(\gamma_0\) is the local spectral index at \(E_0\).
- \(d\) is the local curvature at \(E_0\)
The \(b=0\) case corresponds to a LogParabola with \(\alpha=\gamma_0\) and \(\beta = d/2\).
ConstantValue:
Example: XML Model Definition
A constant-valued function, independent of energy.
![]()
where
- Value =

Gaussian:
Example: XML Model Definition
A Gaussian function that can be used to model an emission line.
![]()
where
- Prefactor =

- Mean =
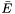
- Sigma =
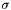
BandFunction:
Example: XML Model Definition
This function is used to model GRB spectra.
![]()
where
- norm =

- alpha =
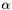
- beta =
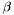
- Ep =
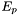
DMFitFunction:
This function is used to fit for putative dark matter signals (as described in Jeltema & Profumo 2008)
Example: XML Model Definition
The functional form for the flux is:
<σv> N0 (Br F(M,C0) + (1 - Br F(M,C1)))
where the values of F(M,C) are tabulated in the file $FERMI_DIR/data/Likelihood/gammamc_dif.dat
The XML parameters are:
- norm = N0, the J-factor. (Units are GeV2/cm5)
- sigmav = <σv>, the thermally averaged cross section, i.e., the thing we care about (Units are cm3 s-1 )
- mass = M, the mass of the DM particle (Units are GeV)
- bratio = Br, branching ratio into decay channel0 (and 1- the branching ratio into decay channel1)
- channel0 = C0, primary decay channel
- channel1 = C1, secondary decay channel (optional)
The decay channels take integer codes, the map is:
- 1 : "e+e-"
- 2 : "mu+mu-"
- 3 : "tau+tau-"
- 4 : "bb-bar"
- 5 : "tt-bar"
- 6 : "gluons"
- 7 : "W+W-"
- 8 : "Z Z"
- 9 : "cc-bar"
- 10 : "cosmo bb-bar"
- 11 : "cosmo gam-gam"
FileFunction:
Example: XML Model Definition
A function defined using an input ASCII file with columns of energy and differential flux values. The energy units are assumed to be MeV and the flux values are assumed to ![]() for a point source and
for a point source and ![]() for a diffuse source. The sole parameter is a multiplicative normalization.
for a diffuse source. The sole parameter is a multiplicative normalization.
![]()
where
- Normalization =

Spatial Models
NOTE: Free flag attributes are currently disabled for spatial model parameters since fitting for these parameters has not been implemented (primarily due to the enormous overhead associated with computing the energy-dependent response functions for each source component).
Four spatial models are available:
- SkyDirFunction - describes a direction on the sky and is used for point sources or radial models.
- ConstantValue - provides a constant value regardless of what argument value it takes. (In the current context, ConstantValue is used to model the isotropic diffuse emission. As a function, however, ConstantValue is fairly general and can even be used in a spectral model; as it is when the spatial model is a MapCubeFunction.)
- SpatialMap - uses a FITS image file as a template for determining the distribution of photons on the sky. (XML Example)
- MapCubeFunction - used for diffuse sources that are modeled by a 3 dimensional FITS map (two sky coordinates and energy), thereby allowing arbitrary spectral variation as a function of sky position. (XML Example)
Last updated by: Nestor Mirabal - 02/14/2018
