Fermi Gamma-ray Space Telescope

Energy Dispersion

The energy dispersion of the LAT is defined in terms of the fractional difference between the reconstructed energy (E') and the true energy (E) of the events.

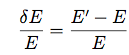
Equation for scaled energy dispersion

The energy dispersion parameterization is fit independently in two-dimensional bins in true energy (E) and inclination angle (θ). The default binning for the energy dispersion parameterization is 4 energy bins per decade, from 0.75 to 6.50 in log(Energy) (corresponding to the range 5.6 MeV to 3.2 TeV), and 8 inclination angle bins, equally spaced from 0.2 to 1.0 in cos(θ). For each bin, a scaled energy dispersion is calculated, binned into a histogram, and then fitted as described below. First, we define

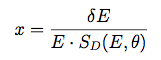
Equation for scaled energy dispersion

where the scaling factor depends on both true energy (E) and true incidence angle (θ):

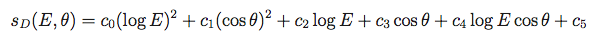
Equation for energy dispersion scaling factor

All 6 parameters have distinct values for different event types. These parameters are stored in the EDISP_SCALING_PARAMS table of the EDISP fits file. In Pass 8 the format of this table has been changed to include only the parameters for the given IRF event type (previously the table contained both FRONT and BACK parameters). The scaling parameters used for the P8R3_V2 IRFs are given in the table below.

Event Type c0 c1 c2 c3 c4 c5
FRONT 0.0195 0.1831 -0.2163 -0.4434 0.0510 0.6621
BACK 0.0167 0.1623 -0.1945 -0.4592 0.0694 0.5899
PSF0/PSF1 0.0195 0.1831 -0.2163 -0.4434 0.0510 0.6621
PSF2/PSF3 0.0167 0.1623 -0.1945 -0.4592 0.0694 0.5899
EDISP0 0.0281 0.4014 -0.1539 -0.2188 -0.0877 0.4510
EDISP1 0.0263 0.2880 -0.1909 -0.2747 0.0380 0.5363
EDISP2 0.0208 0.2226 -0.1770 -0.3102 -0.0045 0.5147
EDISP3 0.0159 0.0770 -0.17189 -0.2900 0.0413 0.4983

A new energy dispersion parameterization has been developed in conjunction with the Pass 8 development. The new parameterization is a combination of two asymmetric exponential power functions normalized to unity. The asymmetric exponential power function (g) is parametrized by four parameters (S,K,B,P) where:

  • S is the sigma of the function
  • K is the skewness parameter
  • B is the bias
  • P is the exponential index

The explicit expression for this base function is:

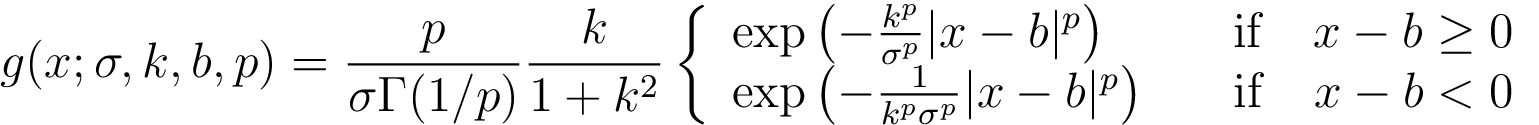
Explicit expression for the LAT's Energy Dispersion function

The final energy dispersion function combines two asymmetric exponential power functions with overall normalization equal to one. To do so we introduce an additional parameter (F) which is the fraction of events in the first asymmetric exponential power function. The full energy dispersion function is thus given by:

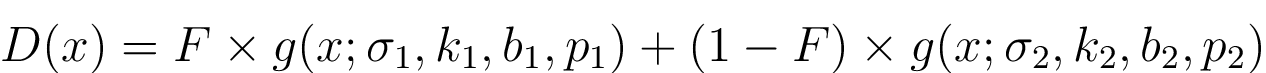
Functional form of the LAT's Energy Dispersion function

Hence the final function depends on 9 parameters: F, S1, K1, BIAS1, PINDEX1, S2, K2, BIAS2, PINDEX2. These parameters are stored in ENERGY DISPERSION table of the EDISP fits file.

The following plot shows a histogram of the scaled deviation for simulated events passing the P8R3_SOURCE_V2::FRONT selection. The best-fit energy dispersion function is shown superimposed as the solid black curve.

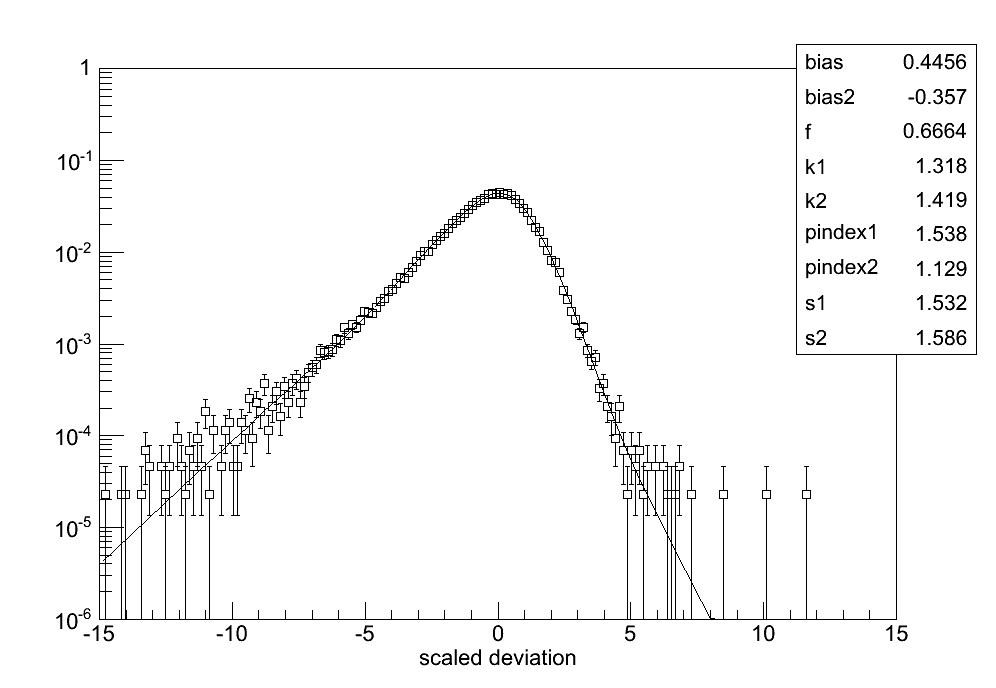
Histogram of scaled deviation for FRONT Source class events

The LAT energy resolution (i.e., the minimum 68% containment interval of the energy dispersion) is of order 5-15% and for broadband spectral analyses the impact of energy dispersion is relatively small (< 5% above 300 MeV). However for studies of bright sources or sharp spectral features the LAT energy resolution may be an important consideration. The Fermitools do not account for the effect of energy dispersion by default. An energy dispersion correction can be enabled for binned likelihood analysis. See the Pass 8 analysis and Energy Dispersion page for information on the recommended practices for accounting for energy dispersion in science analysis.

» Forward to LAT Sensitivity
» Back to Effective Area
» Back to the beginning of the IRFs
» Back to the beginning of the Cicerone